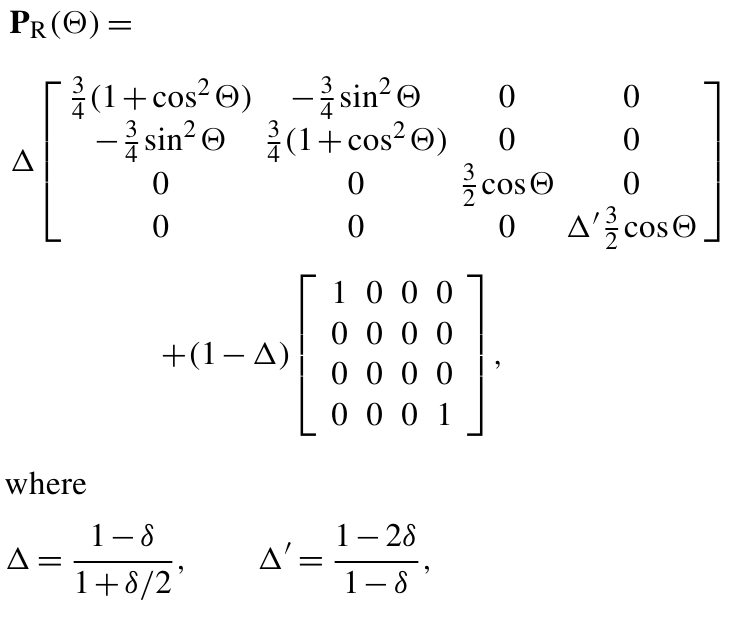Sidebar
Table of Contents
Benchmark dataset for UV-Vis-NIR spectral regions
Monochromatic calculations
Calculations were performed for all combinations of the following parameters:
Wavelengths: 325nm, 450nm, 765nm, 1700m
Viewing angle range: 0° - 60°, 5° increment
Solar zenith angles: 0°, 30°, 60°, 80°
Solar azimuth angles: 0°, 40°, 150°, 220°
Surface albedos: 0, 0.2, 0.8
Each case was computed for the following scenarios with and without polarization.
Output: Normalized radiance (I Q U V)/E_0
Clear sky (Rayleigh scattering)
Rayleigh scattering coefficients were computed according to Bodhaine 1999, Eq. 29 for a 100 layer equidistant model atmosphere (US Standard, Anderson 1986). The following files include the coefficients as calculated on the 101 levels or averaged for the 100 model layers:
csca_rayleigh_layer.dat
csca_rayleigh_level.dat
The Rayleigh scattering matrix is well known:
θ is the scattering angle and δ the depolarization factor, which is also calculated from Bodhaine 1999: depol.dat
Vector calculations
The following plots show the results of all vector calculations:
results_comparison.pdf
Lines correspond to the SCIATRAN results and crosses to MYSTIC results. The results agree within the Monte Carlo noise (<0.5% for I, <1% for Q, U, V is zero for Rayleigh scattering).
The SCIATRAN results (analytical) may be used as benchmark, we do not provide MYSTIC results because of Monte Carlo noise.
Benchmark data (SCIATRAN): st_rayleigh.nc
Scalar calculations
Plots: results_comparison_scalar.pdf
Lines correspond to the SCIATRAN results and crosses to DISORT results. The agreement is better than 0.005%.
Benchmark data (DISORT): result_rayleigh_scalar.nc
Clear sky (Rayleigh scattering + absorption)
In a real atmosphere the molecules also absorb radiation, the next scenarios are for a realistic molecular atmosphere including scattering and absorption. The absorption coefficients are calculated using the libRadtran model which includes absorption coefficients of all relevant atmospheric species. For 1700 nm the absorpion parameterization based on representative wavelengths (Gasteiger et al 2013) was used:
cabs_mol_level.dat
cabs_mol_layer.dat
The agreement of the models is similar to the cases without absorption.
Vector calculations
Plots: results_absorption.pdf
Benchmark results (SCIATRAN): st_rayleigh_abs.nc
Scalar calculations
Plots: results_absorption_scalar.pdf
Benchmark results (DISORT): result_rayleigh_abs_scalar.nc
Cloud (water cloud, optical properties provided)
Cloud in 2-3 km altitude, optical thickness: 10
Optical properties are provided in the following files:
netcdf-Format: wc_325.mie.cdf wc_450.mie.cdf wc_765.mie.cdf wc_1700.mie.cdf
ascii-Format: wc_325.mie.dat wc_450.mie.dat wc_765.mie.dat wc_1700.mie.dat
The variable “phase” includes the phase matrix, as a function of the scattering angle (variable “theta”). The 4×4 scattering phase matrix for spherical droplets has four non-zero elements, which are stored in the following order:
| P1 | P2 | 0 | 0 |
| P2 | P1 | 0 | 0 |
| 0 | 0 | P3 | P4 |
| 0 | 0 | -P4 | P3 |
The single scattering albedo and the extinction coefficient are also stored in the files.
Plots: results_cloud_noabs.pdf
Benchmark results (SCIATRAN): st_cld.nc
High spectral resolution calculations
O2A band (755 - 775 nm) (clear)
The absorption coefficients in the O2A band have been calculated for the midlatitude-summer atmosphere using the ARTS model. They are based on the HITRAN2004 line cataloque.
As input the absorption coefficients abs_coeff_lbl_o2a.dat or alternatively the absorption optical thicknesses of each model layer moltau_o2a.nc may be used.
The spectra are calculated for all viewing geometries and solar zenith angles defined above. The surface albedo was constantly 0.2.
Plots: results_absorption_spectra.pdf
Benchmark results (SCIATRAN): st_o2_spec.nc