How large does an ensemble need to be?
19.05.2022
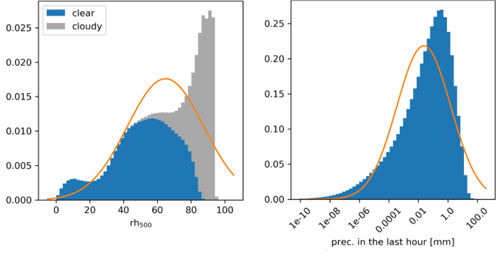
A large number of forecast variables at different lead times were examined, and their distributions could be classified into three categories: quasi-normal (e.g. tropospheric temperature), highly skewed (e.g. precipitation), and mixtures (e.g. humidity). Dependence on ensemble size was examined in comparison to the asymptotic convergence law that the sampling error decreases proportional to N-1/2 for large enough ensemble size N, independent of the underlying distribution shape. The asymptotic convergence behaviour was observed for the ensemble mean of all forecast variables, even for ensemble sizes less than 10. For the ensemble standard deviation, sizes of up to 100 were required for the convergence law to apply. In contrast, there was no clear sign of convergence for the 95th percentile even with 1000 members. Methods such as neighbourhood statistics or prediction of area-averaged quantities were found to improve accuracy, but only for variables with random small-scale variability, such as convective precipitation.
Craig G. C., M. Puh, C. Keil, K. Tempest, T. Necker, J. Ruiz, M. Weissmann and T. Miyoshi (2022). Distributions and convergence of forecast variables in a 1000 member convectionpermitting ensemble. https://doi.org/10.1002/qj.4305

