Model error
Model error in data assimilation for geophysical circulation models
In order to compute optimal weights of background and observations, any data assimilation scheme needs accurate estimates of the corresponding error covariance matrices. In ensemble Kalman filters, the background error covariance matrix is sampled by an ensemble of geophysical model runs. However, since any numerical model itself suffers from errors and also since the number of ensemble members typically used is much smaller (10-100) than the dimension of the phase space of a typical atmopheric circulation model (>106), the entire uncertainty cannot be captured this way.
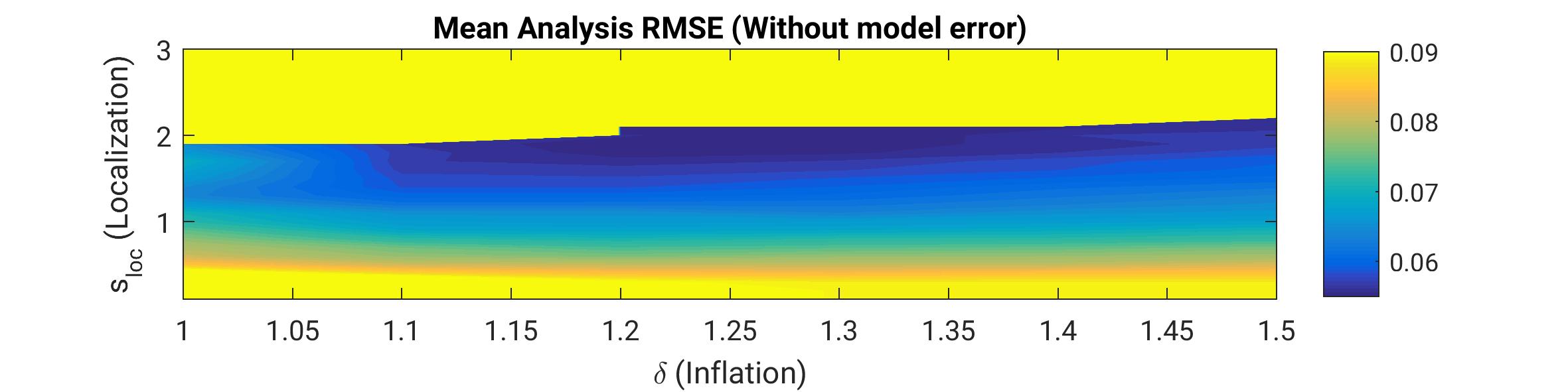
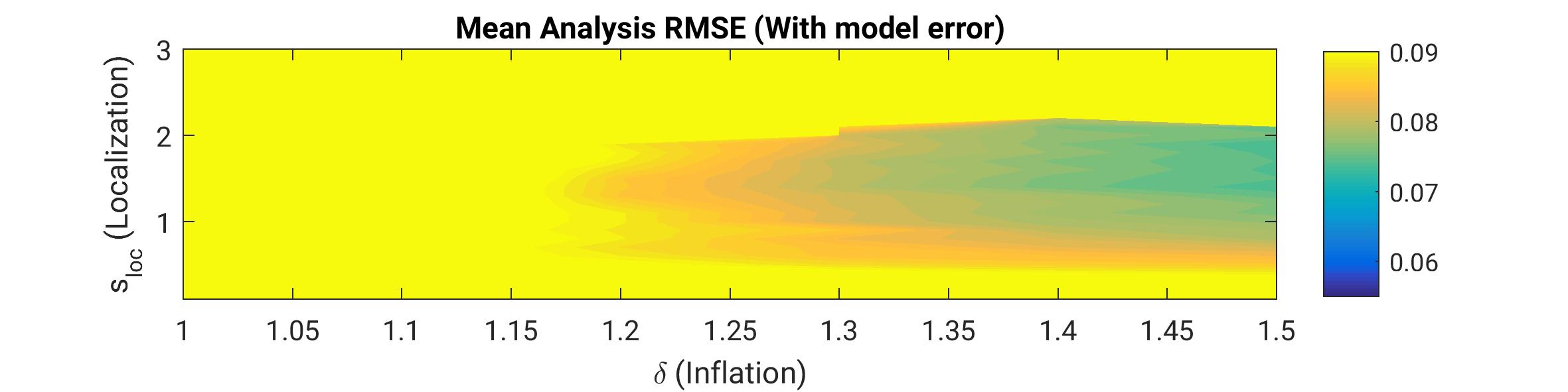
This work unit investigates methods for correcting these deficiencies as for example localization, as well as multiplicative and additive inflation. While the former two are designed to address the sampling error, the latter deals with model error itself as illustrated in the figure below. In a perfect model experiment with a low-dimensional toy model (Lorenz'96) an optimal combination of localization and multiplicative inflation yields the lowest error (blue region in the upper panel). If however model error exists, the optimal multiplicative inflation factor becomes very large while the RMSE remains higher (lower panel) than in perfect model experiment. As an alternative approach, additive inflation can be implemented to overcome that shortcoming. This approach is ongoing research together with an implementation for the regional weather forecasting model COSMO of German Weather Service (Deutscher Wetterdienst DWD).